5.1.2.3 Q31 (1.31) Format

In Q31 format, the Most Significant bit is defined as a sign bit and the radix point is implied to lie just after the sign bit followed by the fractional value. This format is commonly referred to as 1.31 or Q31 format, where 1 is the number of bits used to represent the integer portion of the number, and 31 is the number of bits used to represent the fractional portion. The range of an N-bit two’s complement fraction with this implied radix point is -1.0 to (1 - 2^1-N ). For a 32-bit fraction, the 1.31 data range is -1.0 (0x80000000) to +0. 9999999995343387 (0x7FFFFFFF) with a precision of 4.656612873077393e-10.

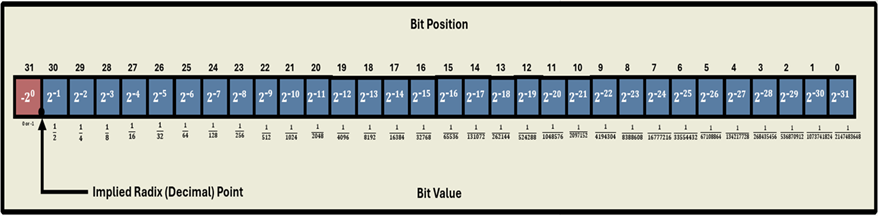
The following table shows the conversion of a two’s complement 32-bit integer +1610612736 to Q31 value +0.75.

Table 5-3. Conversion of a Two’s Complement 32-Bit Integer to Q31

Binary		Dec		Q31
0	0 x 2-31		0 x 20	0
1	1 x 230	1073741824	0 x 21	0.5
1	1 x 229	536870912	0 x 22	0.25
0	0 x 228		0 x 23	0
0	0 x 227		0 x 24	0
0	0 x 226		0 x 25	0
0	0 x 225		0 x 26	0
0	0 x 224		0 x 27	0
0	0 x 223		0 x 28	0
0	0 x 222		0 x 29	0
0	0 x 221		0 x 210	0
0	0 x 220		0 x 211	0
0	0 x 219		0 x 212	0
0	0 x 218		0 x 213	0
0	0 x 217		0 x 214	0
0	0 x 216		0 x 215	0
0	0 x 215		0 x 216	0
0	0 x 214		0 x 217	0
0	0 x 213		0 x 218	0
0	0 x 212		0 x 219	0
0	0 x 211		0 x 220	0
0	0 x 210		0 x 221	0
0	0 x 29		0 x 222	0
0	0 x 28		0 x 223	0
0	0 x 27		0 x 224	0
0	0 x 26		0 x 225	0
0	0 x 25		0 x 226	0
0	0 x 24		0 x 227	0
0	0 x 23		0 x 228	0
0	0 x 22		0 x 229	0
0	0 x 21		0 x 230	0
0	0 x 20		0 x 231	0
	SUM	1610612736	SUM	0.75
= Radix point