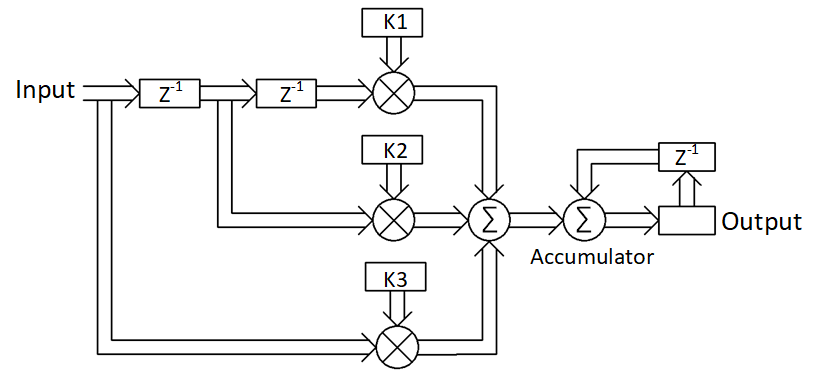
3 PIC Control

In control theory, a PID controller takes the difference between the desired and actual outputs and converts them into three terms: proportional, integral and differential. The proportional term is a simple multiplication of the difference. The integral term is a summation of the current and previous inputs. And, the differential term is the difference between the current and previous inputs. The proportional term drives the output toward a minimal difference between desired and actual outputs. The integral term drives the output toward a zero difference between the desired and actual output by integrating long term non-zero error terms. The differential term acts as a stabilizing factor, which slows the approach to a zero error to prevent overshoot.

For an in-depth explanation of a PID system, refer to TB3136: PID Control on PIC16F161X by using a PID Peripheral for a derivation of the discrete-time PID function. In this application note, it skips to the end and shows the final function. See Figure 3-1.
Figure 3-1. PID System Function
Each (Z-1) is a single sample time delay, i.e., the value is from the previous calculation. This, combined with the accumulate function on the output, provides the proportional, integral and differential terms for the PID.
Note: The Kp, Ki and Kd terms don’t translate directly from the frequency domain. Instead, the following are the constants for the time domain version of the PID function. The term “T” is the sampling period of the discrete-time system. For this design, T = 100 ms, the sample time for the tachometer frequency counter circuit.
K 1 = K p + K i T + K d T
K 2 = K p − 2 K d T
K 3 = K d T