3 Vibration

One of the characteristics of quartz is that any movement or change in forces on the crystal can change the frequency. This is typically represented in data sheets in units of ppm or ppb/g. For example, a common spec might indicate that a 10MHz crystal will change approximately 1ppm/g. The sensitivity means that when the crystal is exposed to mechanical vibration, it will have a higher phase noise due to these random slight movements. This occurs in helicopters, jets, or even in locations that are in close proximity to other mechanical vibrating elements, like a cooling fan.

The change in respect to the frequency of vibration can be calculated by the equation below. In this equation, ‘Γ’ represents the acceleration sensitivity of the crystal, “a” represents the acceleration seen by the crystal, “f_O” is the frequency of oscillation and “f_V” is the frequency of the vibration.

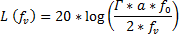
For a sinusoidal vibration, “a” is the peak applied vibration level in units of g, and L(f_V) is expressed in units of dBc. In most real-world applications, vibration is completely random. With random vibration, the power is randomly distributed over a range of frequencies, phases, and amplitudes, and it is more practical to have acceleration represented by its power spectral density (PSD). For random vibration, “a” is the square-root of twice the PSD and represented in units of g²/Hz and, therefore, L(f_V) is expressed in units of dBc/Hz.

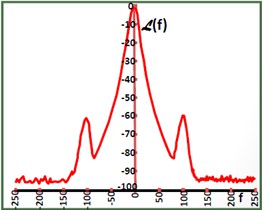
Below are examples of vibration on an oscillator. In Figure 3-4, we see sinusoidal vibration producing spectral lines at ±f_V from the carrier. As these vibrations increase in magnitude, the sidebands will eventually overpower the carrier, causing a collapse. In Figure 3-5, we see the effects of random vibration being applied along the x-axis of an oscillator, and how it can severely impact phase noise performance.

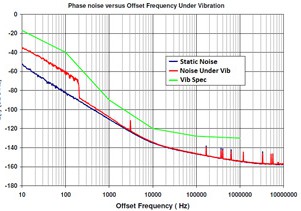
Methods most commonly used in order to reduce vibration-induced phase noise can be as simple as isolating the vibration (using rubber, foam, or springs) and using more rigid materials (ceramic versus aluminum) to as complicated as active vibration cancellation. One such method would be that, while an oscillator is under vibration, an estimate of a complex-conjugate (same amplitude, opposite phase) signal can be generated from accelerometer signals and used to modulate the oscillator’s output phase in such a way as to suppress or cancel the induced sidebands.