2.4 Averaging
The conventional meaning of averaging is adding m samples, and dividing the result by m, which is referred to as normal averaging. Averaging data from an ADC measurement is equivalent to a low-pass filter and has the advantage of attenuating signal fluctuation or noise, and it will flatten out peaks in the input signal. The moving average method is very often used to do this. It works by taking m readings, place them in a cyclic queue and average the most recent m. This will give a slight time delay because each sample is a representation of the last m samples. This can be done with or without overlapping windows. The figure below shows seven (Av1-Av7) independently moving average results without overlapping.
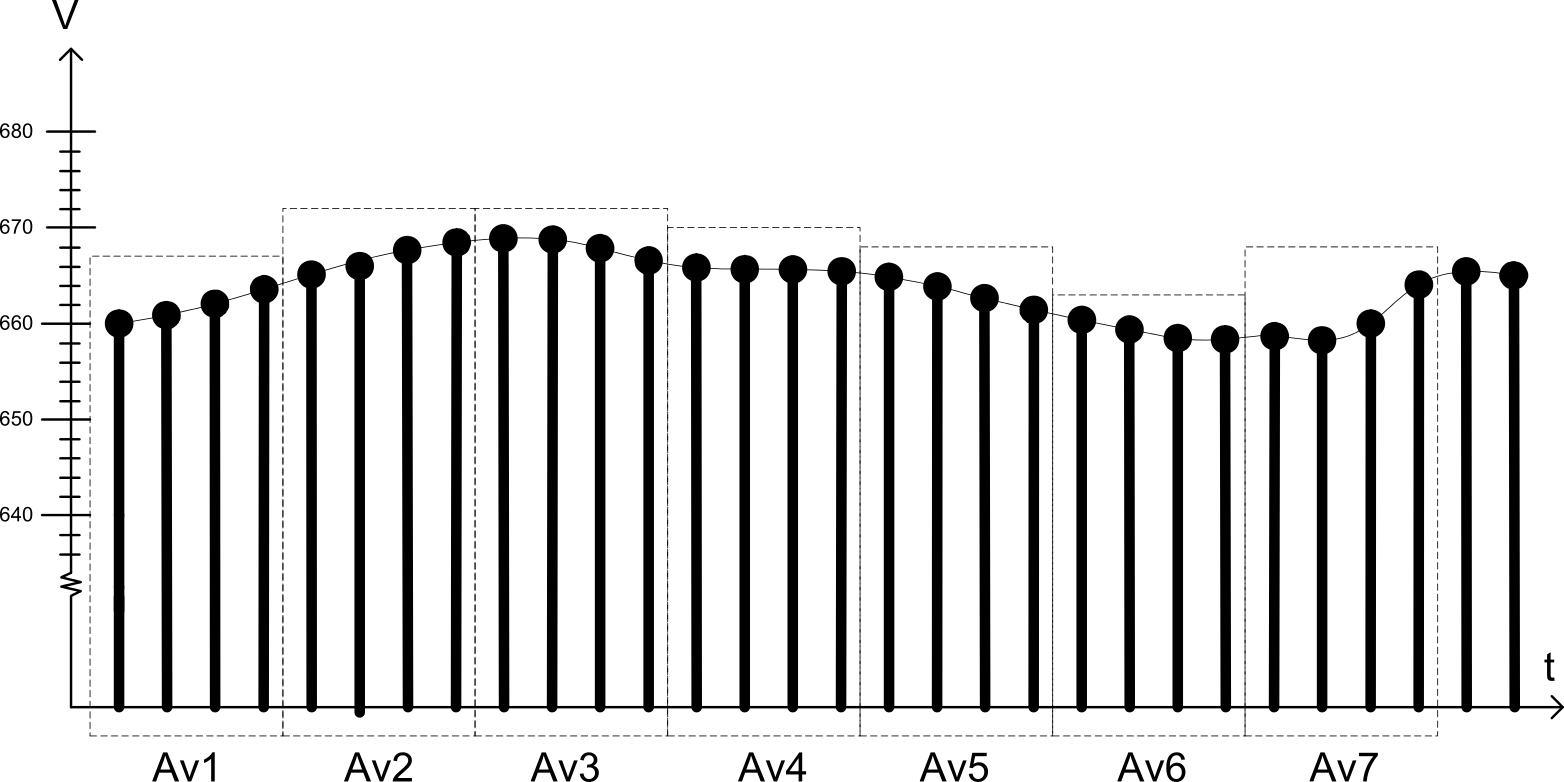
It is important to remember that normal averaging does not increase the resolution of the conversion. Decimation, or interpolation, is the averaging method, which combined with oversampling increases the resolution.
The extra samples, m, achieved by oversampling the signal are summed up, just as in normal averaging, but the result is not divided by m as in normal averaging. Instead, the result is right shifted by n, where n is the desired extra bit of resolution, to scale the answer correctly. Right shifting a binary number once is equal to dividing the binary number by a factor of 2.
As seen from Equation 2-2, increasing the resolution from 10 to 12 bits (that is, additional 2-bit resolution), requires the summation of 4^2 (16) 10-bit values. A sum of 16 10-bit values generates a 14-bit result where the last two bits are not expected to hold valuable information.
To get ‘back’ to 12-bit representation, it is necessary to scale the result. The scale factor, sf, given by the equation below, is the factor, which the sum of 4n samples should be divided by, to scale the result properly. n is the desired number of extra bit.
As explained in the case above (increasing resolution from 10-bit to 12-bit), the scaling factor, sf, is 2^2, which is equal to 4.
