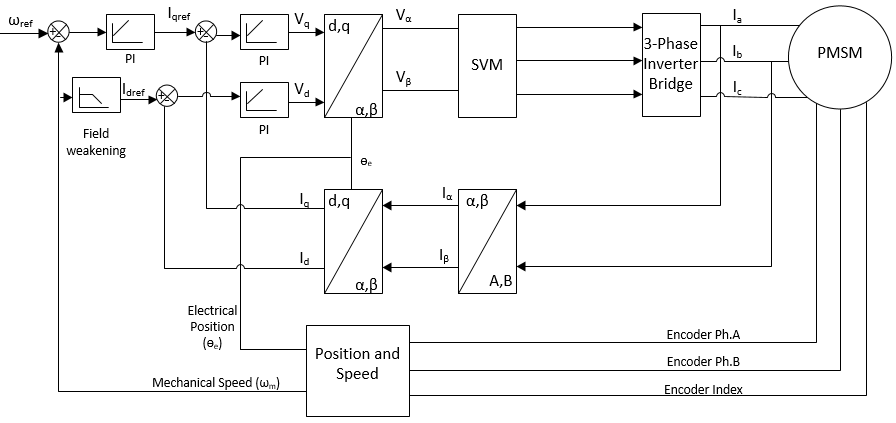
2 Block Diagram of Sensored FOC of PMSM

The control can be summarized as follows:

• The three-phase stator currents are measured. For a motor with balanced three-phase windings, only two currents are sufficient to be measured. The third current can be calculated by the following equation:

  ${\displaystyle i_a+i_b+i_c=0}$

• The three-phase currents are converted to a stationary two-axis system. This conversion provides the variables i_α and i_β from the measured i_a, i_b, i_c values. The values i_α, i_β are time-varying quadrature current values as viewed from the perspective of the stator.
• The stationary two-axis coordinate system is rotated to align with the rotor flux using a transformation angle measured at the last iteration of the control loop. This conversion provides the i_d, i_q variables from i_α and i_β. The values i_d and i_q are the quadrature currents transformed to the rotating coordinate system. For steady state conditions, i_d, i_q are constant.
• Reference values of currents are explained below:
  • i_d reference: controls rotor magnetizing flux
  • i_qreference: controls the torque output of the motor
• The error signals are fed to PI controllers. The output of the controllers provide v_d, v_q, which are voltage vectors that will be applied to the motor.
• A new transformation angle is measured from the encoder pulses input. This new angle guides the FOC algorithm as to where to place the next voltage vector.
• The v_d, v_q output values from the PI controllers are rotated back to the stationary reference frame using the new angle. This calculation provides the next quadrature voltage values v_α,v_β.
• The v_α,v_β values are used to calculate the new PWM duty cycle values which will generate the desired voltage vector
• Mechanical speed (ω_m) is calculated after every discrete PWM cycle

The FOC software is implemented in the ADC interrupt service routine after the end of the conversion of data. It runs at the same rate as the PWM switching frequency.

Field Oriented control of PMSM in the form of a block diagram is shown in the following figure.