37.3.6.13 Quick Verifying an ECDSA Signature (Compliant with FIPS 186-2)
Purpose
This service is used to verify an ECDSA signature following the FIPS 186-2. It performs the second step of the Signature Verification using Quick Dual Multiplying to perform computation.
A hash value (HashVal) must be provided as input, it has to be previously computed from the message whose signature is verified using a secure hash algorithm.
As second significant input, the Signature is provided to be checked.
This service checks the signature and fills the status accordingly.
How to Use the Service
Description
The operation performed is:
Verify = EcDsaVerifySignature(PtA, HashVal, Signature, CurveParameters, PublicKey)
The points used for this operation are represented in different coordinate systems.
In this computation, the following parameters need to be provided (such that u2MaxLength = max(u2ModLength, u2ScalarLength)):
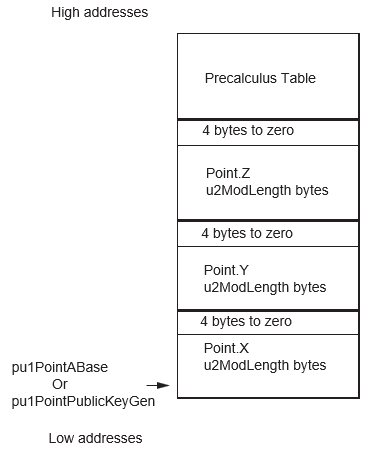
- A the input point is filled with the affine values (X,Y) and Z = 1 (pointed by {pu1PointABase,(3*(u2ModLength + 4)) * (2(WA-2))})
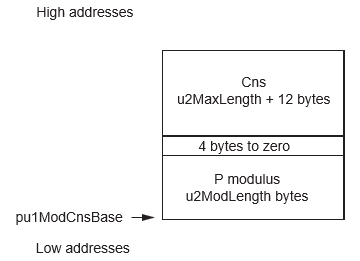
- P the modulus filled and Cns the working space for the Fast Modular Constant not initialized (pointed by {pu1ModBase, u2ModLength + u2MaxLength + 16})
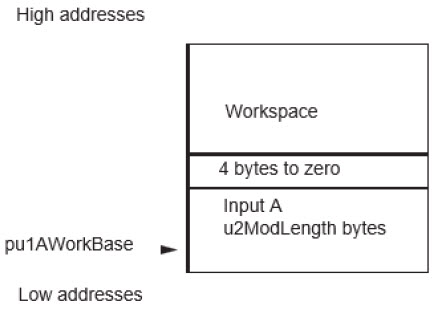
- The a parameter relative to the elliptic curve filled and workspace not initialized (pointed by {pu1AWorkBase,8*u2MaxLength + u2ModLength + 48})
- The order of the Point A on the elliptic curve (pointed by {pu1OrderPointBase,u2ScalarLength +4})
- HashVal the hash value beforehand generated and filled (pointed by {pu1HashBase,u2MaxLength +4})
- The Public Key point is filled in “mixed” coordinates (X,Y) with the affine values and Z = 1 (pointed by {nu1PointPublicKeyGen, (3*(u2ModLength + 4)) * (2(WB-2))})
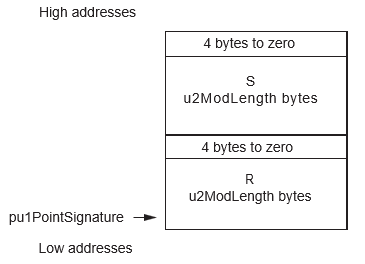
- The input signature (R,S), even if it is not a Point, is represented in memory like a point in affine coordinates (X,Y) (pointed by {nu1PointSignature, 2*u2ScalarLength + 8})
The operation consists of obtaining a V value with all input parameters and checks that V equals the provided R. If all is correct and the signature is the good one, the status is set to PUKCL_OK. If all is correct and the signature is wrong, the status is set to PUKCL_WRONG_SIGNATURE. If an error occurs, the status is set to the corresponding error value (see Status Returned Values below).
Parameters Definition
To place the parameters correctly the maximum of u2ModLength and u2ScalarLength must be calculated: u2MaxLength = max(u2ModLength, u2ScalarLength)
WA is the Point A window size and WB is the Point Public Key window size (see Options below for details).
max() service which takes the maximum of
two values. Ensure that the pu1 type is a pointer on 4 bytes and
contains the full address (see Aligned Significant Length for details). | Parameter | Type | Direction | Location | Data Length | Before Executing the Service | After Executing the Service |
|---|---|---|---|---|---|---|
| pu1ModCnsBase | pu1 | I | Crypto RAM |
u2ModLength + 4 + u2MaxLength + 12 | Base of modulus P | Base of modulus P |
| u2Option | u2 | I | – | – | Option related to the called service (see below) | – |
| u2ModLength | u2 | I | – | – | Length of modulus P | Length of modulus P |
| pu1OrderPointBase | pu1 | I | Crypto RAM | u2ScalarLength + 4 | Order of the Point A in the elliptic curve | Unchanged |
| pu1PointSignature | pu1 | I | Any RAM | 2*u2ScalarLength + 8 | Signature(r, s) | Corrupted |
| pu1HashBase (see Note 1) | pu1 | I | Crypto RAM | u2MaxLength + 4 | Base of the hash value resulting from the previous SHA | Corrupted |
| u2ScalarLength | u2 | I | – | – | Length of scalar | Length of scalar |
| pu1PointABase | pu1 | I/O | Crypto RAM |
(3*u2ModLength + 12) * (2(WA-2)) | Generator point | Corrupted |
| pu1PointPublicKeyGen | pu1 |
I/O | Crypto RAM |
(3*u2ModLength + 12) * (2(WB-2)) | Public Key point | Corrupted |
| pu1AWorkBase | pu1 | I | Crypto RAM | (u2ModLength + 4) + (8*u2MaxLength + 44) | Parameter a of the elliptic curve and Workspace | Corrupted |
- 1. The hash value calculus is defined by the ECDSA norm and depends on the elliptic curve domain parameters. To construct the input parameter, the 4 Most Significant Bytes must be set to zero.
A suggested parameters placement in Crypto RAM is:
- ModCnsBase
- OrderPointBase
- Signature may be placed here or in Classical RAM
- HashBase
- PointABase
- PointPublicKeyGen
- AWorkBase
Options
The options are set by the u2Options input parameter, which is composed of:
- the mandatory windows sizes WA (window for Point A) and WB (window for Point Public Key)
- the indication of the presence of the Point Signature in system RAM
The u2Options number is calculated by an “Inclusive OR” of the options. Some Examples in C language are:
// Point Signature in system RAM// The Point A window size is 3// The Point Public Key window size is 4PUKCL(u2Options) = PUKCL_ZPECCMUL_SCAL_IN_CLASSIC_RAM |PUKCL_ZPECCMUL_WINSIZE_A_VAL_TO_OPT(3) |PUKCL_ZPECCMUL_WINSIZE_B_VAL_TO_OPT(4);// Point Signature in the Cryptographic RAM// The Point A window size is 2// The Point Public Key window size is 5PUKCL(u2Options) = PUKCL_ZPECCMUL_WINSIZE_A_VAL_TO_OPT(2) |PUKCL_ZPECCMUL_WINSIZE_B_VAL_TO_OPT(5);
For this service, many window sizes are possible. The window sizes in bits are those of the windowing method used for the scalar multiplying.
The choice of the window sizes is a balance between the size of the parameters and the computation time:
- Increasing the window size increases the precomputation table size.
- Increasing the window size to the optimum reduces the computation time.
The following table details the estimated windows WA and WB optimum and possible for some curves.
| Curve Size (bits) | Optimum Window size | Possible Window Sizes (WA, WB) or (WB, WA) |
|---|---|---|
| 192 | 5 | 5, 5 |
| 256 | 5 | 5, 5 |
| 384 | 6 | 5, 5 |
| 521 | 6 | 4, 5 |
The following table details the size of the point and the precomputation table, depending on the chosen window size option.
| Option Specified | Point and Precomputation Table Size |
|---|---|
| PUKCL_ZPECCMUL_WINSIZE_A_VAL_TO_OPT(WA) WA in [2, 15] | (3*(u2ModLength + 4)) * (2(WA-2)) |
| PUKCL_ZPECCMUL_WINSIZE_B_VAL_TO_OPT(WB) WB in [2, 15] | (3*(u2ModLength + 4)) * (2(WB-2)) |
The Point Signature can be located in PUKCC RAM or in system RAM. If the Point Signature is entirely in system RAM with no part in PUKCC RAM this can be signaled by us ing the option PUKCL_ZPECCMUL_SCAL_IN_CLASSIC_RAM. In all other cases this option must not be used.
The following table describes this option.
| Option | Purpose |
|
PUKCL_ZPECCMUL_SCAL_IN_CLASSIC_RAM | The Point Signature can be located in Crypto RAM or in system RAM. If the Point Signature is entirely in system RAM with no part in PUKCC RAM this can be signaled by using this option. In all other cases this option must not be used. |
Code Example
PUKCL_PARAM PUKCLParam;
PPUKCL_PARAM pvPUKCLParam = &PUKCLParam;
PUKCL(u2Option) = <Point Signature location and windows sizes>;
PUKCL_ZpEcDsaQuickVerify(pu1ModCnsBase) = <Base of the ram location of P and Cns>;
PUKCL_ZpEcDsaQuickVerify(u2ModLength) = <Byte length of P>;
PUKCL_ZpEcDsaQuickVerify(pu1PointABase) = <Base of the ram location of the A point>;
PUKCL_ZpEcDsaQuickVerify(pu1PointPublicKeyGen) = <Base of the Public Key>;
PUKCL_ZpEcDsaQuickVerify(pu1PointSignature) = <Base of the Signature (r, s)>;
PUKCL_ZpEcDsaQuickVerify(pu1OrderPointBase) = <Base of the order of the A point>;
PUKCL_ZpEcDsaQuickVerify(pu1AWorkBase) = <Base of the ram location of the parameter A of the elliptic curve and workspace>;
PUKCL_ZpEcDsaQuickVerify(pu1HashBase) = <Base of the SHA resulting hash>;
PUKCL_ZpEcDsaQuickVerify(u2ScalarLength) = <Byte length of R and S in Point Signature>;
. . .
// vPUKCL_Process() is a macro command, which populates the service name
// and then calls the library...
vPUKCL_Process(ZpEcDsaQuickVerify, pvPUKCLParam);
if (PUKCL(u2Status) == PUKCL_OK)
{
...
}
else
if ( PUKCL(u2Status) = PUKCL_WRONG_SIGNATURE )
{
...
}
else // Manage the error
Constraints
No overlapping between either input and output are allowed. The following conditions must be avoided to ensure that the service works correctly:
- pu1ModCnsBase, pu1PointABase, pu1PointPublicKeyGen, pu1PointSignature,pu1OrderPointBase, pu1AWorkBase or pu1HashBase are not aligned on 32-bit boundaries
- {pu1ModCnsBase, u2ModLength + 4 + u2MaxLength + 12}, {pu1PointABase, (3 * u2ModLength + 12)* (2(WA-2))}, {pu1PointPublicKeyGen, (3 * u2ModLength + 12) * (2(WPub-2))}, {pu1OrderPointBase, u2ScalarLength + 4}, {nu1ABase, u2ModLength + 4}, {pu1AWorkBase, (u2ModLength + 4) + (8 * u2MaxLength + 44)} or {nu1HashBase, u2ScalarLength + 4} are not in Crypto RAM
- u2ModLength is either: < 12, > 0xffc or not a 32-bit length
- All overlapping between {pu1ModCnsBase, u2ModLength + 4 + u2MaxLength + 12},{pu1PointABase, (3 * u2ModLength + 12) * (2(WA-2))}, {pu1PointPublicKeyGen, (3 * u2ModLength + 12) *(2(WPub-2))}, {pu1OrderPointBase, u2ScalarLength + 4}, {pu1PointSignature, 2 * u2ScalarLength + 8}, {nu1ABase, u2ModLength + 4}, {pu1AWorkBase, (u2ModLength + 4) + (8 * u2MaxLength + 44)} and {nu1HashBase, u2ScalarLength + 4}
Status Returned Values
| Returned Status | Importance | Meaning |
|---|---|---|
| PUKCL_OK | – | The computation passed without problem. The signature is the good one. |
| PUKCL_WRONG_SIGNATURE | Warning | The signature is wrong. |
Parameter Placement
The parameters’ placement is described in detail in the following figures.